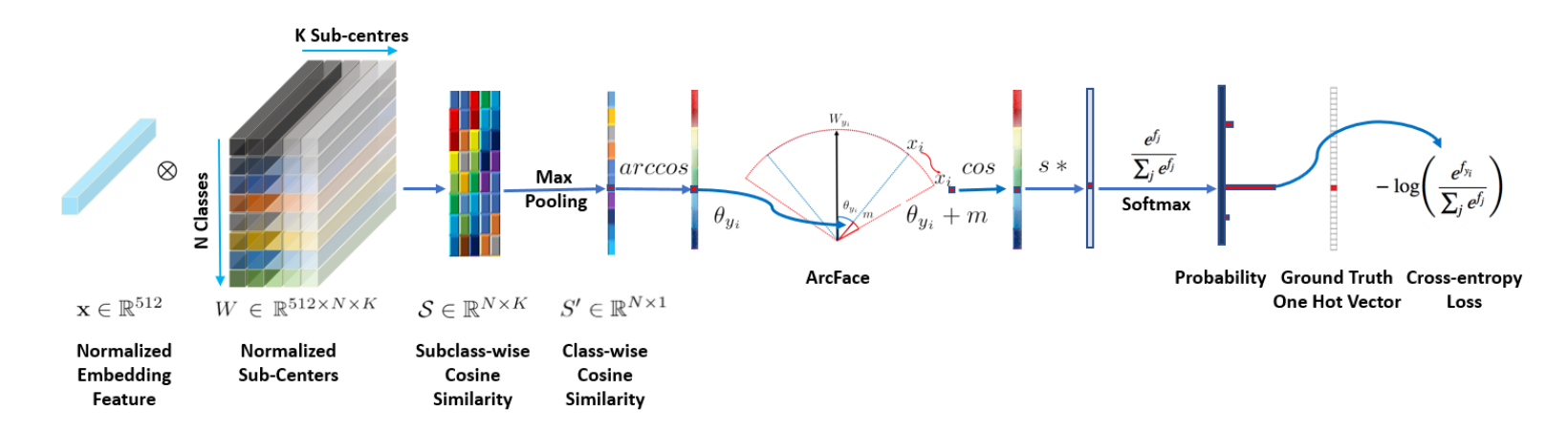
ArcFace Loss
Here’s the table of contents:
Introduction
Facial recognition technology has witnessed significant advancements in recent years, thanks to the power of deep learning. These models have shown remarkable accuracy and robustness in recognizing and verifying individuals based on their facial features. One of the breakthroughs in this domain is the introduction of ArcFace, a deep face recognition algorithm that incorporates the Additive Angular Margin Loss. In this blog post, we will delve into the technical details of ArcFace and understand how it improves deep face recognition systems.
Understanding Face Recognition
Face recognition involves the identification and verification of individuals based on their facial characteristics. Traditional approaches relied on manually engineered features, which often struggled with variations in lighting conditions, poses, and facial expressions. Deep learning models, on the other hand, have the ability to learn discriminative representations directly from raw images, enabling more accurate and robust face recognition.
Deep Face Recognition with ArcFace
ArcFace is an innovative deep face recognition algorithm proposed by Jiankang Deng, et al. in their 2019 paper, “ArcFace: Additive Angular Margin Loss for Deep Face Recognition.” It addresses the challenge of effectively learning discriminative face features by incorporating an angular margin into the loss function.
Additive Angular Margin Loss
The core idea behind ArcFace is to introduce an angular margin that pushes the learned features of different classes apart in the angular space. By enforcing greater separability between classes, ArcFace enhances the model’s ability to discriminate between similar faces.
Let’s dive into the mathematics behind the Additive Angular Margin Loss. Consider a deep neural network with parameters \(\theta\) and a fully connected layer that produces an embedding vector \(f \in \mathbb{R}^d\) for a given input face image. The embedding vector is normalized to lie on the surface of a hypersphere:
\[\|f\|_2 = 1\]where \(\| \cdot \|_2\) denotes the Euclidean norm. The normalized feature vector can be represented as:
\[f = \frac{W^T x}{\|W^T x\|_2}\]where \(W \in \mathbb{R}^{d \times m}\) is the weight matrix of the fully connected layer, \(x\) is the input image, and \(m\) represents the number of classes.
The output logits of the network for class \(i\) can be obtained by taking the dot product between the normalized feature vector \(f\) and the weight vector \(W_i\) corresponding to class \(i\). Mathematically, this can be expressed as:
\[s_i = W_i^T f\]where \(W_i\) represents the \(i\)-th column of the weight matrix \(W\).
To introduce an angular margin, ArcFace uses the cosine function to calculate the similarity between the feature vector \(f\) and each weight vector \(W_i\). The modified logits \(s_i'\) can be computed as:
\[s_i' = \cos(\theta_i) = \frac{e^{\cos(\theta_i)}}{\sum_{j=1}^m e^{\cos(\theta_j)}}\]where \(\theta_i\) denotes the angle between the feature vector \(f\) and the weight vector \(W_i\).
The Additive Angular Margin Loss can be formulated as follows:
\[L = -\frac{1}{N} \sum_{i=1}^N \log \left(\frac{e^{\cos(\theta_{y_i} + m)}}{e^{\cos(\theta_{y_i} + m)} + \sum_{j=1, j \neq y_i}^m e^{\cos(\ theta_j)}}\right)\]where \(N\) is the batch size, \(y_i\) is the ground truth label for the \(i\)-th example, and \(m\) represents the angular margin. The loss function aims to maximize the angular margin between the correct class and the other classes.
Geometric Interpretation
To gain a better understanding of how ArcFace works, we can interpret it geometrically. By mapping the feature vectors onto a hypersphere, ArcFace encourages the features of the same class to be concentrated around a specific angle. The angular margin pushes these features away from the decision boundary, thus enhancing inter-class separability.
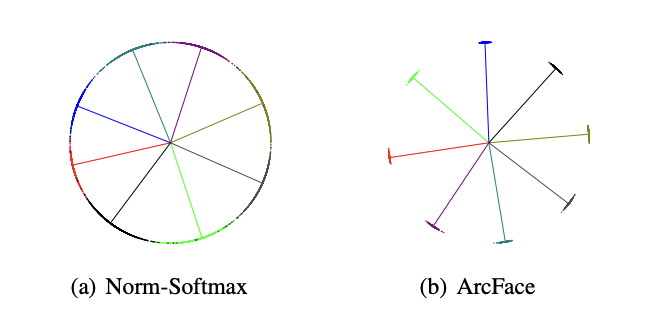
In the above image, we can visualize how ArcFace pushes the feature vectors of different classes away from the decision boundary. The angular margin helps maintain clear boundaries between different identities.
Training Procedure
Training a face recognition model with ArcFace involves optimizing the network parameters \(\theta\) to minimize the Additive Angular Margin Loss. During training, face images are passed through a deep convolutional neural network (CNN) to extract high-level features. These features are then normalized and mapped onto a hypersphere. Finally, the ArcFace loss is computed and used to update the network parameters through backpropagation.
ArcFace Loss Implementation in PyTorch
class ArcFace(nn.Module):
def __init__(self, feature_in, feature_out=24, margin=0.3, scale=64):
super().__init__()
self.feature_in = feature_in
self.feature_out = feature_out
self.scale = scale
self.margin = margin
self.weights = nn.Parameter(torch.FloatTensor(feature_out, feature_in))
nn.init.xavier_normal_(self.weights)
The ArcFace class is defined as a subclass of nn.Module. It takes several parameters: feature_in (dimensionality of input features), feature_out (number of output classes), margin (angular margin value), and scale (scaling factor for the logits).
In the constructor __init__, the class initializes its attributes and creates a learnable weight matrix self.weights of size (feature_out, feature_in). The weights are initialized using the Xavier initialization method.
def forward(self, features, targets):
cos_theta = F.linear(features, F.normalize(self.weights), bias=None)
cos_theta = cos_theta.clip(-1+1e-7, 1-1e-7)
The forward method performs the forward pass of the ArcFace loss function. It takes two arguments: features (input features) and targets (ground truth labels).
Inside the method, F.linear performs the linear transformation of the input features using the learnable weight matrix self.weights. The features are then normalized using F.normalize. The resulting cosine similarities cos_theta are clipped to ensure they stay within the range [-1+1e-7, 1-1e-7] to avoid numerical instabilities.
arc_cos = torch.acos(cos_theta)
M = F.one_hot(targets, num_classes=self.feature_out) * self.margin
arc_cos += M
Next, torch.acos is applied to calculate the arccosine of cos_theta, which gives the angles in radians. The variable M is computed as the one-hot encoded ground truth labels multiplied by the angular margin self.margin. This introduces the angular margin to the arccosine values. Finally, arc_cos is updated by adding M to it.
cos_theta_2 = torch.cos(arc_cos)
logits = cos_theta_2 * self.scale
return logits
In the final steps, torch.cos is applied to the updated arc_cos to get the cosine of the new angles. These values are multiplied by the scaling factor self.scale to obtain the final logits. The logits represent the model’s predictions for each class. The method returns the logits.
The code provided implements the ArcFace loss function and can be used within a larger neural network model for deep face recognition. To experiment with arcface check full implementation on MNIST Dataset on Kaggle Notebook.
Benefits of ArcFace
ArcFace brings several benefits to deep face recognition systems:
-
Improved Discrimination: By incorporating the Additive Angular Margin Loss, ArcFace enhances the model’s ability to discriminate between similar faces, leading to improved accuracy.
-
Robustness to Variations: ArcFace’s discriminative features are more robust to variations in lighting conditions, poses, and facial expressions, making it suitable for real-world scenarios.
-
Large-scale Identification: ArcFace performs exceptionally well in large-scale face identification tasks, where the number of identities is vast. The angular margin helps maintain clear boundaries between identities, reducing the chances of misclassification.
-
Interpretability: ArcFace’s geometric interpretation provides researchers and practitioners with a clear understanding of how the model learns to discriminate between different faces, making it easier to analyze and interpret its behavior.
Comparison with Contrastive Loss
Another popular loss function used in face recognition is the Contrastive Loss. While both ArcFace and Contrastive Loss aim to learn discriminative face features, they differ in their approaches.
Contrastive Loss encourages similar face images to have small distances in the feature space, while dissimilar face images should have large distances. It achieves this by minimizing the distance between positive pairs (images of the same identity) and maximizing the distance between negative pairs (images of different identities). Contrastive Loss operates on pairs of images and requires a predefined threshold to determine whether the pairs are positive or negative.
On the other hand, ArcFace incorporates the Additive Angular Margin Loss, which directly optimizes the angular margin between different classes. This approach explicitly introduces a margin into the loss function, pushing the features of different classes apart in the angular space. ArcFace does not rely on pairs of images but rather considers the angular relationships between the feature vectors and the weight vectors associated with each class.
Compared to Contrastive Loss, ArcFace has several advantages.
- ArcFace does not require the definition of a threshold to distinguish between positive and negative pairs, making it more straightforward to implement.
- ArcFace explicitly learns the discriminative angular relationships between classes, leading to improved inter-class separability.
- In Contrastive Loss there is a combinatorial explosion in the number of face pairs especially for large-scale datasets, leading to a significant increase in the number of iteration steps.
- ArcFace training can be done without semi-hard sample mining.
- ArcFace has shown superior performance in large-scale face identification tasks, where the number of identities is vast.
To evaluate the performance of ArcFace in comparison to the Contrastive Loss, we can examine their results on the MNIST dataset, a widely-used benchmark for image classification tasks. The MNIST dataset consists of 60,000 training images and 10,000 test images of handwritten digits from 0 to 9.
For the ArcFace implementation, the accuracy achieved on the MNIST dataset is 99.371% (as reported in the Kaggle link: ArcFace on MNIST Data). This indicates that ArcFace successfully discriminates between the different digit classes with high accuracy.
On the other hand, the Contrastive Loss implementation achieves an accuracy of 99.246% on the same MNIST dataset (as reported in the Kaggle link: Contrastive on MNIST Data). While this is also a commendable accuracy, it is slightly lower than the accuracy achieved by ArcFace.
The higher accuracy achieved by ArcFace on the MNIST dataset demonstrates its effectiveness in capturing discriminative features for face recognition tasks. By explicitly incorporating an angular margin into the loss function, ArcFace pushes the features of different classes apart in the angular space, leading to improved inter-class separability.
Conclusion
ArcFace, with its Additive Angular Margin Loss, has emerged as a powerful technique for deep face recognition. By incorporating an angular margin into the loss function, ArcFace enhances the discrimination between classes and enables the model to learn more discriminative features. Its geometric interpretation and training procedure make it a valuable tool for researchers and practitioners in the field of facial recognition. With further advancements and research, ArcFace has the potential to drive breakthroughs in face recognition technology and its diverse applications.
